CONSTRUCCION DE LA RECTA EULER

 

   CONSTRUCCION DE LA RECTA DE EULER

            Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos. Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. En los triángulos se puede denotar un grupo de rectas y puntos muy importantes. Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

RECTAS DE MEDIATRICES 

1.   Para poder formar las rectas mediatrices en la aplicación de GeoGebra se necesita primero marcar los puntos en donde se quiere marcar el triángulo.

2. Posteriormente para poder unirlos se marcaran los segmentos, en la misma aplicación marca la opción. 

3. Después utilizaremos la opción de recta perpendicular, esto servirá para marcar el centro del triangulo.

4. Ya que están las rectas marcadas, hay que señalar la mediatriz, a esta se le da el nombre de circuncentro.

5. En el sexto recuadro de opciones (Circunferencia[centro, punto], se utilizara para marcar la circunferencia del triangulo  

6. Por ultimo, la misma programación marcara las coordenada de cada segmento.  

Rectas de mediatrices 

CINCUNCENTRO

Es el punto de corte de las mediatrices de un triángulo. Las mediatrices son las rectas perpendiculares a cada lado y que pasan por el centro del mismo.

Para poder marcar el circuncentro solo damos en la opción de intersección y lo unimos en el centro de intersección de punto común de las líneas, automáticamente el programa le da un valor, en este caso G.  

MEDIANAS 

Se hace el mismo proceso para formar el triangulo, solo que en este caso se marcaran las mediatrices y los puntos de intersección, al marcarlos cada linea se leda el nombre de mediana, dependiendo de orden se le da ha mediana1, mediana 2, mediana 3,

BARICENTRO 

Es el punto de corte de las medianas de un triángulo. Las medianas son las rectas que pasan por el centro de cada lado del triángulo y corta al vértice contrario.

ALTURA

En este se lleva el mismo proceso, para  marcar las rectas, se utiliza el formato de recta perpendicular, al marcarlo en cada punto (ABC), se posicionan solo en su lugar correspondiente, para marcar el ortocentro se utiliza la mediatriz.

ORTOCENTRO

Es el punto de corte de las alturas de un triángulo. Las alturas son las rectas perpendiculares a cada lado que pasa por el vértice contrario.

RECTAS BICECTRICES 

INCENTRO

LA RECTA DE EULER

La recta de Euler de un triángulo es aquella que contiene al ortocentro, al circuncentro y al baricentro del mismo. Se llama así en honor al matemático suizo Leonhard Euler, quien descubrió este hecho a mediados del siglo XVIII.

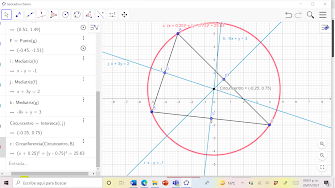
La figura consiste en una gráfica cartesiana localizando tres puntos de los vértices de un triángulo, representando las rectas de la mediana de color naranja y su respectivo punto de intercepción el baricentro, las rectas de la altura de color verde y su punto de intercepción el ortocentro y, las rectas de la mediatriz de color azul claro y su punto de intercepción el circuncentro. Y la recta de Euler en color negro, que se obtiene uniendo los puntos ortocentro, baricentro y, circuncentro.